Commutative property

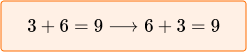
Here you will learn about the commutative property, including what it is, and how to use it to solve problems.

Students will first learn about the commutative property as part of operations and algebraic thinking in 3rd grade.

What is the commutative property?

The commutative property states that when you add or multiply numbers, you can change the order of the numbers and the answer will still be the same.

When adding, you can change the order
of the addends:

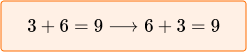
Notice that even with a different order,
the sum is the same.

This is also true when multiplying numbers.

When multiplying, you can change the
order of the numbers:

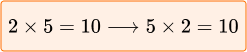
Notice that even with a different order,
the product is the same.

The commutative property can be used to create friendly numbers when solving.

Friendly numbers are numbers that are easy to add or multiply mentally – like multiples of 10.

The commutative property lets us change the order and create friendlier numbers.

10 + 25 is easier to solve mentally than 3 + 25 + 7 = 28 + 7.

The commutative property lets us regroup and create friendlier numbers.

10 \times 8 is easier to solve mentally than 2 \times 8 \times 5=16 \times 5.

The commutative property can also be referred to as the commutative property of addition and the commutative property of multiplication, or more generally as the commutative law.

What is the commutative property?

Common Core State Standards

How does this relate to 3rd grade math?

• Grade 3 – Operations and Algebraic Thinking (3.OA.B.5)
  Apply properties of operations as strategies to multiply and divide.
  Examples: If 6 \times 4 = 24 is known, then 4 \times 6 = 24 is also known. (Commutative property of multiplication.)
  3 \times 5 \times 2 can be found by 3 \times 5 = 15, then 15 \times 2 = 30, or by 5 \times 2 = 10, then 3 \times 10 = 30. (Associative property of multiplication.)
  Knowing that 8 \times 5 = 40 and 8 \times 2 = 16, one can find 8 \times 7 as 8 \times (5 + 2) = (8 \times 5) + (8 \times 2) = 40 + 16 = 56. (Distributive property.)

[FREE] Properties of Equality Check for Understanding Quiz (Grade 3 to 6)

Use this quiz to check your grade 3 to 6 students’ understanding of properties of equality. 10+ questions with answers covering a range of 3rd, 5th and 6th grade properties of equality topics to identify areas of strength and support!

[FREE] Properties of Equality Check for Understanding Quiz (Grade 3 to 6)

Use this quiz to check your grade 3 to 6 students’ understanding of properties of equality. 10+ questions with answers covering a range of 3rd, 5th and 6th grade properties of equality topics to identify areas of strength and support!

How to use the commutative property

In order to use the commutative property:

1. Check to see that the operation is addition or multiplication.
2. Change the order of the numbers and solve.

Commutative property examples

Example 1: simple commutative property with addition

Give an example of the commutative property using 4 + 9.

1. Check to see that the operation is addition or multiplication.

All the numbers are being added, so the commutative property can be used.

2 Change the order of the numbers and solve.

4 + 9 = 13 \; \longrightarrow \; 9 + 4 = 13

Changing the order in the equation does not change the sum.

Example 2: simple commutative property with multiplication

Give an example of the commutative property using 10 \times 6.

Check to see that the operation is addition or multiplication.

All the numbers are being multiplied, so the commutative property can be used.

Change the order of the numbers and solve.

Changing the order in the equation does not change the product.

Example 3: commutative property – addition with friendly numbers

Use the commutative property to create a friendly number and solve 6 + 32 + 14.

Check to see that the operation is addition or multiplication.

All the numbers are being added, so the commutative property can be used.

Change the order of the numbers and solve.

Example 4: commutative property – multiplication with friendly numbers

Use the commutative property to create a friendly number and solve 3 \times 8 \times 3.

Check to see that the operation is addition or multiplication.

All the numbers are being multiplied, so the commutative property can be used.

Change the order of the numbers and solve.

Notice that when multiplying, friendly numbers can also be single digit numbers. If you know your basic facts, it is easier to solve 9 \times 8 than solving 3 \times 8 \times 3=24 \times 3.

Example 5: commutative property – addition with friendly numbers

Use the commutative property to create a friendly number and solve 41 + 17 + 9.

Check to see that the operation is addition or multiplication.

All the numbers are being added, so the commutative property can be used.

Change the order of the numbers and solve.

Example 6: commutative property – multiplication with friendly numbers

Use the commutative property to create a friendly number and solve 3 \times 5 \times 4.

Check to see that the operation is addition or multiplication.

All the numbers are being multiplied, so the commutative property can be used.

Change the order of the numbers and solve.

Notice that when multiplying, friendly numbers can also be numbers that are basic facts. If you have memorized the basic multiplication facts from 1-12, it is easier to solve 12 \times 5 than solving 3 \times 5 \times 4=15 \times 4.

Teaching tips for the commutative property

• Be intentional about choosing problems where the commutative property makes solving easier, since it is not always useful or necessary in all solving situations.

• Instead of just telling students the commutative property definition, draw attention to examples of the commutative property when they naturally occur in daily math activities. Record the different examples you see in the classroom on an anchor chart. Over time, students will start recognizing and using the property on their own. Then, after there are sufficient examples, you can introduce students to the property name and definition by using their own examples.

• Include plenty of student discourse around this property so that students understand changing the order of numbers when adding or multiplying does not change the final result. This could include students sharing their thinking or critiquing the thinking of others.

Easy mistakes to make

• Using the commutative property for subtraction or division
  The commutative property only works when changing the order of the numbers doesn’t change the answer. This is not true for subtraction or division and they are considered non-commutative arithmetic operations.
  For example,
  11-5 = 6 \; AND \; 5-11 = -6
  Changing the order of the numbers, changes the answer.

Thinking there is only one way to use the commutative property to solve with friendly numbers
Sometimes there is more than one way to use the commutative property when solving.
For example,

• Confusing the order of operations
  Equations are always solved moving from left to right. It is not necessary to formally introduce students to the order of operations, but they need to understand and read equations in this way. Otherwise the commutative property may not mean anything to them.

Related properties of equality lessons

This commutative property topic guide is part of our series on properties of equality. You may find it helpful to start with the main properties of equality topic guide for a summary of what to expect or use the step-by-step guides below for further detail on individual topics. Other related topic guides in this series include:

• Properties of equality
• Order of operations
• Associative property
• Distributive property

Practice commutative property questions

1. Which of the following equations shows the commutative property?

The commutative property says that changing the order in the equation does not change the product.

11 \times 6=66 \; \longrightarrow \; 6 \times 11=66

2. Which of the following equations shows the commutative property?

The commutative property says that changing the order in the equation does not change the sum.

\begin & 5+11+9 \hspace \longrightarrow \hspace 9+11+5 \\\\ & =16+9 \hspace =20+5 \\\\ & =25 \hspace =25 \end

3. Which of the following equations shows how to solve 2 \times 9 \times 5 using the commutative property?

The commutative property says that changing the order in the equation does not change the product.

4. Which of the following equations shows how to solve 37 + 28 + 23 using the commutative property?

The commutative property says that changing the order in the equation does not change the sum.

5. Which of the following equations shows how to solve 8 \times 4 \times 5 using the commutative property to create a friendly number?

The commutative property says that changing the order in the equation does not change the product. Friendly numbers are numbers that are easy to multiply mentally – like multiples of 10.

6. Which of the following equations shows how to solve 16+18+22 using the commutative property to create a friendly number?

The commutative property says that changing the order in the equation does not change the sum. Friendly numbers are numbers that are easy to multiply mentally – like multiples of 10.

Commutative property FAQs

No, you can solve the numbers as they appear in the equation, without changing the order. The commutative property just gives you flexibility to add or multiply in a different order.

Does the commutative property work with other groupings of numbers besides natural numbers and whole numbers?

Yes, the commutative property can be used with integers, rational numbers and any real number, as long as they are all being added or multiplied.

The associative property of addition states that you can change the grouping of numbers when adding (using parentheses) and the sum will still be the same. The order of operations changes, but not the written order of the numbers in the equation. The commutative property of addition says you can change the written order of the numbers when adding and the sum will still be the same.

It is one of the properties of numbers for mathematical operations. This property states that any number added to 0 will still result in the same number (0 + a = a) or any number multiplied by 1 will still result in the same number (1 \times a=a).

The next lessons are

• Addition and subtraction
• Multiplication and division
• Types of numbers

Still stuck?

At Third Space Learning, we specialize in helping teachers and school leaders to provide personalized math support for more of their students through high-quality, online one-on-one math tutoring delivered by subject experts.

Each week, our tutors support thousands of students who are at risk of not meeting their grade-level expectations, and help accelerate their progress and boost their confidence.

Find out how we can help your students achieve success with our math tutoring programs.